隔了一段時(shí)間，大家還記不記得上次所學(xué)的支路電流法是什么呀？什么？不記得啦？那你們就得好好反思一下了，肯定是習(xí)題做得還不夠，接下來(lái)怎么做你們懂了吧~

這次的學(xué)習(xí)分享又是一個(gè)新的知識(shí)點(diǎn)了，它就是支路電流法的進(jìn)化版：網(wǎng)孔電流法。曹老師在《電工基礎(chǔ)》中依然是花費(fèi)了兩個(gè)課時(shí)為我們講解這部分內(nèi)容，大家可要好好學(xué)習(xí)，天天向上喲！

學(xué)習(xí)網(wǎng)孔法之前，我們先來(lái)學(xué)習(xí)一下關(guān)于它的一些定義吧。如下圖12-1所示，結(jié)合之前的支路電流法，我們把支路電流全部用網(wǎng)孔電流取代，那么所列的電壓回路方程就會(huì)轉(zhuǎn)換為網(wǎng)孔電流方程的初步形式，電源統(tǒng)一放在方程的右邊，所有網(wǎng)孔的繞行方向宜取相同（可不同）且與網(wǎng)孔電流的參考方向一致（同為順時(shí)針或逆時(shí)針）。

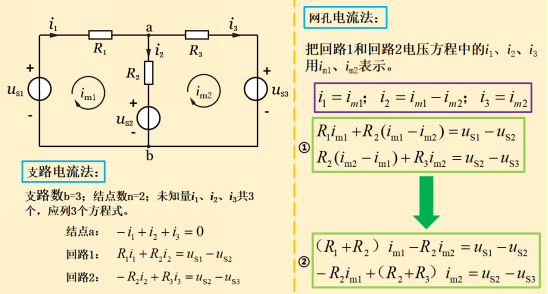
圖12-1

網(wǎng)孔法：以網(wǎng)孔電流為電路的變量來(lái)列寫(xiě)方程的方法。

網(wǎng)孔電流：設(shè)想在每個(gè)網(wǎng)孔中，都有一個(gè)電流沿網(wǎng)孔邊界環(huán)流，這樣一個(gè)在網(wǎng)孔內(nèi)環(huán)行的假想電流叫網(wǎng)孔電流，如圖12-1中的i_m1和i_m2。

從圖12-1我們可以看到，支路1只有網(wǎng)孔電流i_m1流過(guò)，支路電流i₁=i_m1；支路3只有網(wǎng)孔電流i_m2流過(guò)，支路電流i₃=i_m2；但是支路2有2個(gè)網(wǎng)孔電流同時(shí)流過(guò)，在給定的參考方向下，支路電流將是網(wǎng)孔電流的代數(shù)和，即i₂=i_m1-i_m2。

根據(jù)圖12-1中的電路圖，我們把i₁=i_m1、i₂=i_m1-i_m2、i₃=i_m2代入左下角的回路KVL方程，得到右邊的①式，從①式中我們可以看到，沿網(wǎng)孔1繞行的方向列方程時(shí)，R₂上的電壓為R₂(i_m1-i_m2)，其中i_m2前負(fù)號(hào)是因?yàn)殡娏?i>i_m2在R₂上的流動(dòng)方向與i_m1相反的結(jié)果；同理，在網(wǎng)孔2的方程中，沿網(wǎng)孔2繞行的方向，R₂上的電壓則為R₂(i_m2-i_m1)，經(jīng)整理后，就得到右下角的②網(wǎng)孔電流方程。

我們用R₁₁和R₂₂分別代表網(wǎng)孔1和網(wǎng)孔2的自（電）阻，它們分別是網(wǎng)孔1和網(wǎng)孔2中所有電阻之和，即R₁₁=R₁ R₂，R₂₂=R₂ R₃；用R₁₂和R₂₁代表網(wǎng)孔1和網(wǎng)孔2的互（電）阻，即兩個(gè)網(wǎng)孔的共有電阻，在圖12-1的電路圖中，R₁₂=R₂₁=-R₂；用u_s11、u_s22分別代表網(wǎng)孔1和網(wǎng)孔2中所有電壓源的代數(shù)和，稱(chēng)為網(wǎng)孔電源電壓，即u_s11=u_s1-u_s2，u_s22=u_s2-u_s3。終得到如下圖12-2中所示的①方程。

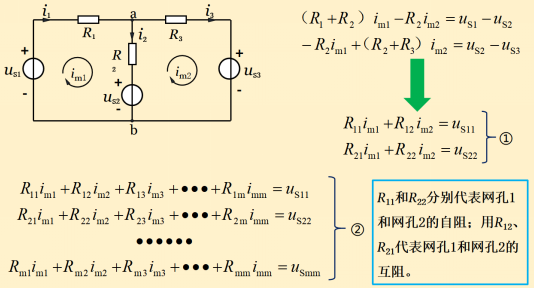
圖12-2

這就是網(wǎng)孔電流方程的一般形式。其中：R₁₁i_m1項(xiàng)代表網(wǎng)孔電流i_m1在網(wǎng)孔1內(nèi)各電阻上引起的電壓之和，R₂₂i_m2項(xiàng)代表網(wǎng)孔電流i_m2在網(wǎng)孔2內(nèi)各電阻上引起的電壓之和。在前文提到，網(wǎng)孔繞行的方向和網(wǎng)孔電流的參考方向取為一致，所以R₁₁和R₂₂總為正值。

當(dāng)兩個(gè)網(wǎng)孔電流在共有電阻（即互阻）上的參考方向相同時(shí)，i_m1在互阻上引起的電壓與網(wǎng)孔2經(jīng)過(guò)互阻的繞行方向一致，同樣的，i_m2引起的電壓與網(wǎng)孔1的繞行方向也一致，互阻上的電壓應(yīng)當(dāng)均為正，反之為負(fù)。把電壓前的“ ”“-”包括在有關(guān)的互阻中，如圖12-2中的R₁₂和R₂₁，此時(shí)它們均為負(fù)，即R₁₂=R₂₁=-R₂，就是因?yàn)?i>i_m1和i_m2在電阻R₂上的方向相反。

依此類(lèi)推，對(duì)具有m個(gè)網(wǎng)孔的平面電路，網(wǎng)孔電流方程的一般形式可以由圖12-2中的①推廣得到，即圖12-2中的②式。式中具有相同下標(biāo)的電阻R₁₁、R₂₂、R₃₃、R_mm等是各網(wǎng)孔的自阻；有不同下標(biāo)的電阻R₁₂、R₁₃、R₂₃、R_m3等是網(wǎng)孔間的互阻。

對(duì)于圖12-2中的②方程式，是網(wǎng)孔電流方程的通用方程式，雖然看起來(lái)很復(fù)雜，但只要把它理解了，其實(shí)是非常簡(jiǎn)單的。顯然，相對(duì)于用支路電流法求解電路，網(wǎng)孔電流法就簡(jiǎn)單多了，所列方程式的個(gè)數(shù)也相對(duì)減少，如圖12-1或圖12-2中的電路圖，共有3條支路，用支路電流法求解時(shí)有3個(gè)未知量（支路電流），需列3個(gè)方程式；但是用網(wǎng)孔電流法求解時(shí)，只有2個(gè)未知量（網(wǎng)孔電流），只需列2個(gè)方程式。

網(wǎng)孔電流法是根據(jù)網(wǎng)孔來(lái)列方程的，且網(wǎng)孔在電路圖中較為直觀，清晰明了，但是電阻和電源較多時(shí)，各網(wǎng)孔的電阻和電源前的正負(fù)號(hào)比較容易弄混，大家在列方程時(shí)要謹(jǐn)慎。

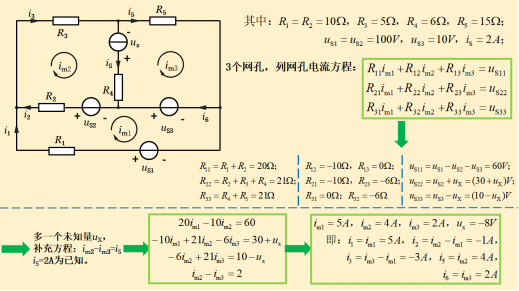
圖12-3

在上一次的學(xué)習(xí)分享中，講到使用支路電流法求解電路時(shí)，提到關(guān)于含有電流源的問(wèn)題的解決方法，就是在列回路電壓方程時(shí)把電流源支路忽略。那么，在網(wǎng)孔電流法中關(guān)于含有電流源支路的問(wèn)題又該怎么解決呢？上圖12-3所示就是一個(gè)用網(wǎng)孔電流法求解含有電流源支路的電路問(wèn)題的例子。

從圖12-3中，我們可以看到，對(duì)于含有電流源的支路，我們把它當(dāng)電壓源處理，又由于電流源的電壓未知，但是它的電流已知，結(jié)合電流源的電流與對(duì)應(yīng)的網(wǎng)孔電流列出補(bǔ)充方程，后共有4個(gè)未知量（網(wǎng)孔電流和電流源電壓）與4個(gè)方程式，顯然，終仍可得到其計(jì)算結(jié)果。

不管是支路電流法或是網(wǎng)孔電流法，都離不開(kāi)基爾霍夫定律的應(yīng)用，這些方法其實(shí)都是基于基爾霍夫電壓定律和電流定律的基礎(chǔ)上演變出來(lái)的。

講到這里，網(wǎng)孔電流法已經(jīng)很清楚了，大家如果還是不理解，那就多看幾次曹老師的課程。曹老師的講解過(guò)程和我的學(xué)習(xí)分享過(guò)程有所不同，大家可以結(jié)合文章與課程進(jìn)行學(xué)習(xí)。（技成培訓(xùn)原創(chuàng)，作者：楊思慧，未經(jīng)授權(quán)不得轉(zhuǎn)載，違者必究?。?/strong>