在上一次學(xué)習(xí)了道菜“基爾霍夫電流定律（KCL）”后，這次我們繼續(xù)學(xué)習(xí)第二道菜“基爾霍夫電壓定律（KVL）”。

在《電工基礎(chǔ)》的第11課時中，“曹大廚”（把曹老師說成廚師，不知道他會不會打我，噓~~）再次給我們展示了他的精湛廚藝，詳細(xì)的講解了基爾霍夫電壓定律以及它的應(yīng)用。

基爾霍夫電壓定律：在任一瞬間，從回路中任一點出發(fā)，沿回路循行一周，則在這個方向上的電位升之和等于電位降之和；或者說：在任一瞬間，沿任一回路循行方向，回路中各段電壓的代數(shù)和恒等于零。

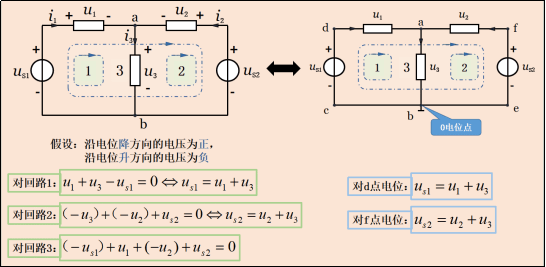
圖9-1就是基爾霍夫電壓定律的電路方程式，按照回路中各元件電壓所列。大家如果列了方程式，但又不知對錯，那么可以根據(jù)之前所學(xué)的電位法去判斷。在這里要強(qiáng)調(diào)的一點就是：在同一電路圖中，各回路的繞行方向應(yīng)保持一致（逆時針或順時針），如圖中的3個回路都是順時針方向；一旦假定電位升的電壓為正或電位降的電壓為正，在之后列方程式時都不可更改，如圖中假定電位降的電壓為正，u₁的電位沿回路繞行方向為降，所以u₁前面為正號。

不知道大家有沒有注意到，對于回路3，我們可以通過回路1、2來計算得到，大家可以自行嘗試計算一下，在這里就不作贅述，另外，回路1、2其實就是我們上次所學(xué)的網(wǎng)孔。

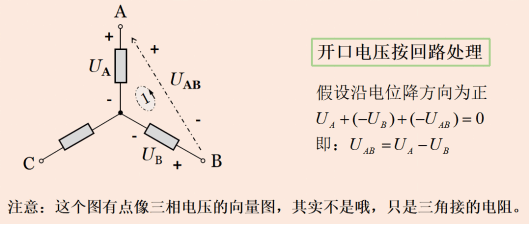
相對于基爾霍夫電流定律中關(guān)于廣義結(jié)點（閉合面）的KCL方程，在基爾霍夫電壓定律中，也有相關(guān)的假想，那就是關(guān)于求回路中非單個元件兩端的電壓，我們可以在所求電壓的兩端用帶無窮大電阻的假想支路連起來。例如圖9-2中求電壓U_AB，在A、B兩端用虛線連起來構(gòu)成回路，再列方程求解。

前文提到，在圖9-1中，回路3的KVL方程可以用回路1、2的KVL方程計算得到。其實，如果我們先列出回路1、3的KVL方程，也可以根據(jù)回路1、3的KVL方程求出回路2的KVL方程。像這種可以通過其他方程得出的方程不是獨立的，但獨立方程并不是絕對的。例如圖9-3所述，獨立方程的個數(shù)是確定的，但是方程的形式并不是絕對的。

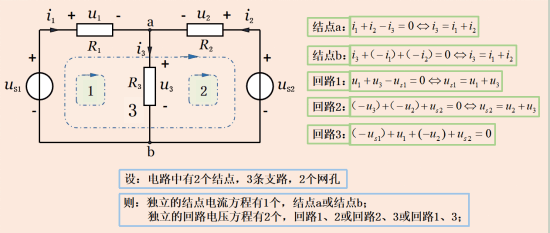
那么，在一個電路中，我們用KCL或KVL列方程時可以列多少個獨立方程呢？可以證明，對于具有N個結(jié)點、B條支路、M個網(wǎng)孔的電路，它的獨立節(jié)點電流方程有（N-1）個，獨立回流電壓方程有（B-N 1）個（或者有M個）。

其實從這里我們可以看到，在有B條支路的電路中，當(dāng)我們求支路電流時，就有了B個未知數(shù)，所以至少需列出B個獨立方程才能求解；結(jié)合KCL和KVL列方程的獨立方程（N-1） （B-N 1）剛好等于B。

顯然，如果電路中增多了一條支路，以此同時它可列的獨立電壓方程也多了一個，照樣可以求解。

對于基爾霍夫定律，給大家來幾道題，學(xué)到這里也差不多了，缺的就是實際解決問題的經(jīng)驗了，大家加油吧！共勉。（技成培訓(xùn)原創(chuàng)，作者：楊思慧，未經(jīng)授權(quán)不得轉(zhuǎn)載，違者必究！）

相關(guān)課程推薦

電工基礎(chǔ)